- 13 Marks
QT – May 2019 – L1 – Q7a – Linear Programming
Formulate a linear programming model for maximizing profit using decision variables and constraints.
Question
Joycarpap Ltd manufactures and sells three models of affordable toys: Car, Joy, and Pap. Each model requires a specific amount of fabrication hours, material worth, and assembly hours as shown in the table below:
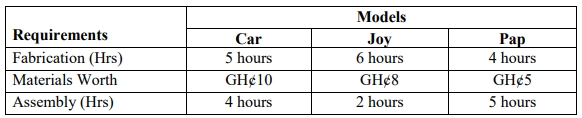
There are 210 fabrication hours available, 170 hours of assembly available, and materials worth GH¢200 in stock. Market research conducted by the company revealed that demand for the toys is such that, in whatever combination of the three models produced, all of the output can be sold within a week.
Each Car contributes GH¢15 to profit, each Joy contributes GH¢20 to profit, and each Pap contributes GH¢14 to profit. Using X1, X2, X3 as decision variables, and S1, S2, S3 as slack variables, and P as total profit:
Required:
i) Formulate a linear programming problem. (4 marks)
ii) Set up the initial Simplex Tableau. (4 marks)
iii) Determine the total profit in the first iteration. (5 marks)
Find Related Questions by Tags, levels, etc.
- Tags: Constraints, Decision Variables, Linear Programming, Profit Maximization, Simplex Method
- Level: Level 1
- Topic: Linear Programming
- Series: MAY 2019